Moment of inertia
Recap
The moment of inertia of a single particle rotating about a centre was introduced in the tutorial on circular motion
I = mr2
It is the rotational of the mass, i.e. it measures the inertial towards angular acceleration.
In chemistry we are most interested in the rotation of molecules, which are essentially made up of point masses, giving
![]()
where ri is the distance of atom i from the axis of rotation.
Consider a molecule rotating about an axis parallel to the z-axis with fixed x and y coordinates. The moment of inertia is
![]()
The moment of inertia may be minimised with respect to the position of the axis, for example
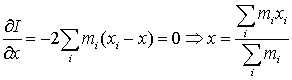
and similarly for y.
Thus the moment of inertia is minimised if the axis passes through the centre of mass of the molecule.
The moment of inertia about any other axis perpendicular to this may be found to be
![]()
where M is the mass of the molecule and d the distance of the axis from the centre of mass.
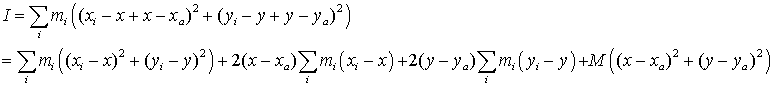
The result follows because the two central sums are zero from the definition of the centre of mass.
The consequence the natural moment of inertia of a molecule is about an axis passing through the centre of mass, and it is straightforard to calculate it for any other axis.
We now calculate the moment of inertia of a diatomic molecule about an axis perpendicular to the bond (this is one of the principal components - see later).
Suppose the z-axis is aligned along the bond direction and the atoms are at z1 and z2. The centre of mass is at coordinate
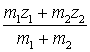
Putting the origin at the centre of mass, atom 1 is at
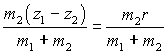
where r is the bond length, and atom 2 at
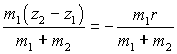
Hence the moment of inertia is
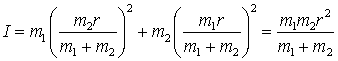
The quantity
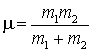
should be familiar from the tutorial on collisions as the reduced mass.
This theorem applies to planar molecules. Suppose the molecule is in the xy plane. The moment of inertia about the z axis is the sum of the moments of inertia about the other two axes. All axes pass through the centre of mass.
It is easy to prove this theorem, taking the centre of mass as the origin
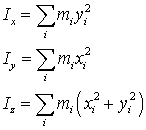
because the z coordinates of all the atoms are zero.
You will not understand this until you have covered matrices and matrix diagonalisation in the maths course.
The analysis above shows clearly that the moment of inertia about an axis depends on the orientation of the axis relative to the molecule. To express the properties of the moment of inertia mathematically it is necessary to express it as a matrix.
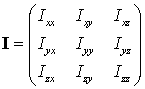
In a coordinate system fixed with respect to the molecule the components of the moment of inertia tensor are defined by
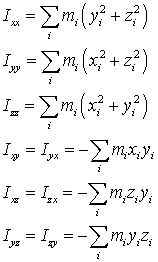
The form of the tensor is proved in many good texts on mechanics, such as Landau and Lifschitz.
The moment of inertia tensor permits the calculation of the moment of inertia about any axis relative to the orientation of the molecule passing through the centre of mass. Given a unit vector k in the direction of the rotation axis the moment of inertia about this axis is given by
![]()
The moment of inertia tensor is a symmetric matrix and it can therefore be diagonalised by an orthogonal transformation of the Cartesian axes. This is a transformation that preserves the lengths of the unit vectors along each axis and their mutual orthogonality. It is essentially a reorientation of the orthogonal axis system.
If the coordinates are reoriented in this way the moment of inertia tensor becomes diagonal, i.e. it has the form
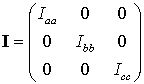
The three diagonal elements are called the principal components of the moment of inertia and the corresponding axes that lead to this diagonal form are the principal axes of the molecule.
The moment of inertia about any other axis can be calculated in the manner described at the end of the previous section.
A molecule in which the three principal components are equal (such as methane) is called a spherical top. If two components are the same it is a symmetric top. If all three components are different it is an asymmetric top.